Efficient Gather-and-scatter Matrix Multiplication Kernel with Triton
This post is to log my implementation of gather-and-scatter matrix multiplication operation with Triton. Click here to jump to the final implementation code. If you are interested in the further implementation of efficient FFN kernel, please refer to this post, where we provide implementation details of our paper Learn to be efficient: Build structured sparsity in large language models.
Intro
Gather-and-scatter matrix multiplication is an essential operation in improving the efficiency of machine learning. For example, if you have a matrix of input features A and you only want to multiply it with a few columns of a weight matrix B, you should skip the other columns to save I/O and computation power.
Some easy-to-implement options to achieve this goal:
- Add a mask to zero-out the unnecessary columns. This won’t save you any time and power.
- Store the required columns of
Bto a new matrixsubB. This will cause additional I/O and memory usage, especially whenBis large.
Therefore, we have to change the kernel of GPU function by passing a index array, asking the GPU to “iterate” over selected columns. Here is a pseudo-code example:
For row in A:
# For col in B:
For i in selected_cols:
col = B.col(i)
c = dot(row, col)
This function is already implemented by CUTLASS library and you can find an example in cutlass/examples/36_gather_scatter_fusion/gather_scatter_fusion.cu. I believe that is the most efficient implementation so far. However, CUTLASS is very complicated and hard to write kernel fusion for beginners. I will make a post on how to generate that into a python operator later, but right now I will show you how to do the same thing with Triton developed by OpenAI.
GEMM in Triton
Thanks to the developers of Triton for providing the example of GEMM. We can modify based on this example to make it compute the selected columns of B.
Below is the example GEMM kernel from Triton’s document
@triton.jit
def matmul_kernel(
# Pointers to matrices
a_ptr, b_ptr, c_ptr,
# Matrix dimensions
M, N, K,
# The stride variables represent how much to increase the ptr by when moving by 1
# element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
# by to get the element one row down (A has M rows).
stride_am, stride_ak, #
stride_bk, stride_bn, #
stride_cm, stride_cn,
# Meta-parameters
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr, #
GROUP_SIZE_M: tl.constexpr, #
):
"""Kernel for computing the matmul C = A x B.
A has shape (M, K), B has shape (K, N) and C has shape (M, N)
"""
# -----------------------------------------------------------
# Map program ids `pid` to the block of C it should compute.
# This is done in a grouped ordering to promote L2 data reuse.
# See above `L2 Cache Optimizations` section for details.
pid = tl.program_id(axis=0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
num_pid_in_group = GROUP_SIZE_M * num_pid_n
group_id = pid // num_pid_in_group
first_pid_m = group_id * GROUP_SIZE_M
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
pid_m = first_pid_m + (pid % group_size_m)
pid_n = (pid % num_pid_in_group) // group_size_m
# ----------------------------------------------------------
# Create pointers for the first blocks of A and B.
# We will advance this pointer as we move in the K direction
# and accumulate
# `a_ptrs` is a block of [BLOCK_SIZE_M, BLOCK_SIZE_K] pointers
# `b_ptrs` is a block of [BLOCK_SIZE_K, BLOCK_SIZE_N] pointers
# See above `Pointer Arithmetic` section for details
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
# -----------------------------------------------------------
# Iterate to compute a block of the C matrix.
# We accumulate into a `[BLOCK_SIZE_M, BLOCK_SIZE_N]` block
# of fp32 values for higher accuracy.
# `accumulator` will be converted back to fp16 after the loop.
accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
# Load the next block of A and B, generate a mask by checking the K dimension.
# If it is out of bounds, set it to 0.
a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
# We accumulate along the K dimension.
accumulator = tl.dot(a, b, accumulator)
# Advance the ptrs to the next K block.
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
c = accumulator.to(tl.float16)
# -----------------------------------------------------------
# Write back the block of the output matrix C with masks.
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
tl.store(c_ptrs, c, mask=c_mask)
To call this kernel, we need two input matrices A and B in size (M, K) (K, N), and prepare an empty output matrix C in (M, N).
def matmul(a, b):
# Check constraints.
assert a.shape[1] == b.shape[0], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
M, K = a.shape
K, N = b.shape
# Allocates output.
c = torch.empty((M, N), device=a.device, dtype=torch.float16)
# 1D launch kernel where each block gets its own program.
grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']), )
matmul_kernel[grid](
a, b, c, #
M, N, K, #
a.stride(0), a.stride(1), #
b.stride(0), b.stride(1), #
c.stride(0), c.stride(1), #
)
return c
Naive Indexed GEMM in Triton
To build gather-and-scatter matrix multiplication, let’s pass a index vector indicating which columns of B matters.
Adding two additional inputs L and l_ptr to the kernel,
def indexed_matmul_kernel(
# Pointers to matrices
a_ptr, b_ptr, c_ptr,
l_ptr, # pointer to the index vector
# Matrix dimensions
M, N, K,
L, # number of indices
# The stride variables represent how much to increase the ptr by when moving by 1
# element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
# by to get the element one row down (A has M rows).
stride_am, stride_ak, #
stride_bk, stride_bn, #
stride_cm, stride_cn,
# Meta-parameters
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr, #
GROUP_SIZE_M: tl.constexpr, #
):
...
The only thing we need to do is replacing offs_bn and offs_cn by offs_bl and offs_cl, and let the grid size be L // BLOCK_SIZE_N.
...
# num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
num_pid_n = tl.cdiv(L, BLOCK_SIZE_N)
...
# offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % L
offs_bl = tl.load(l_ptr + offs_bn)
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
# b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bl[None, :] * stride_bn)
...
# offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
offs_cn = offs_bl
...
In the host function, change the grid size and allocate C to be zeros
def indexed_matmul(a, b, index):
# Check constraints.
assert a.shape[1] == b.shape[0], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
M, K = a.shape
K, N = b.shape
L = index.shape[0]
# Allocates output.
# c = torch.empty((M, N), device=a.device, dtype=torch.float16)
c = torch.zeros((M, N), device=a.device, dtype=torch.float16)
# 1D launch kernel where each block gets its own program.
# grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']), )
grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(L, META['BLOCK_SIZE_N']), )
matmul_kernel[grid](
a, b, c, #
index,
M, N, K, #
L,
a.stride(0), a.stride(1), #
b.stride(0), b.stride(1), #
c.stride(0), c.stride(1), #
)
return c
Let’s set the index be torch.arange(0, N, 2).to('cuda'). Run the code, the result looks like,
# A is a random matrix in (512, 1024)
# B is a random matrix in (1024, 4096)
# C =
tensor([[ 35.3438, 0.0000, 7.6484, ..., 0.0000, 10.9609, 0.0000],
[-55.2812, 0.0000, 36.0625, ..., 0.0000, -75.0000, 0.0000],
[ 9.8203, 0.0000, -12.7266, ..., 0.0000, -11.6641, 0.0000],
...,
[-18.9062, 0.0000, 26.0469, ..., 0.0000, 63.5000, 0.0000],
[ 9.2188, 0.0000, 10.1406, ..., 0.0000, -4.9062, 0.0000],
[-13.7500, 0.0000, -53.5938, ..., 0.0000, -18.4844, 0.0000]],
device='cuda:0', dtype=torch.float16)
The corresponding columns are zeros.
But wait! What about the time consumption?
The time consumption of original GEMM in Triton is 0.48ms, while the indexed one takes 0.65ms, how could it be even slower?
If we take a look to the definition of B = torch.randn((K, N)), this is a row major matrix. However, selecting a part of columns from each row breaks the cacheline coalescing, as a result, the latency of memory loading is even more severe.
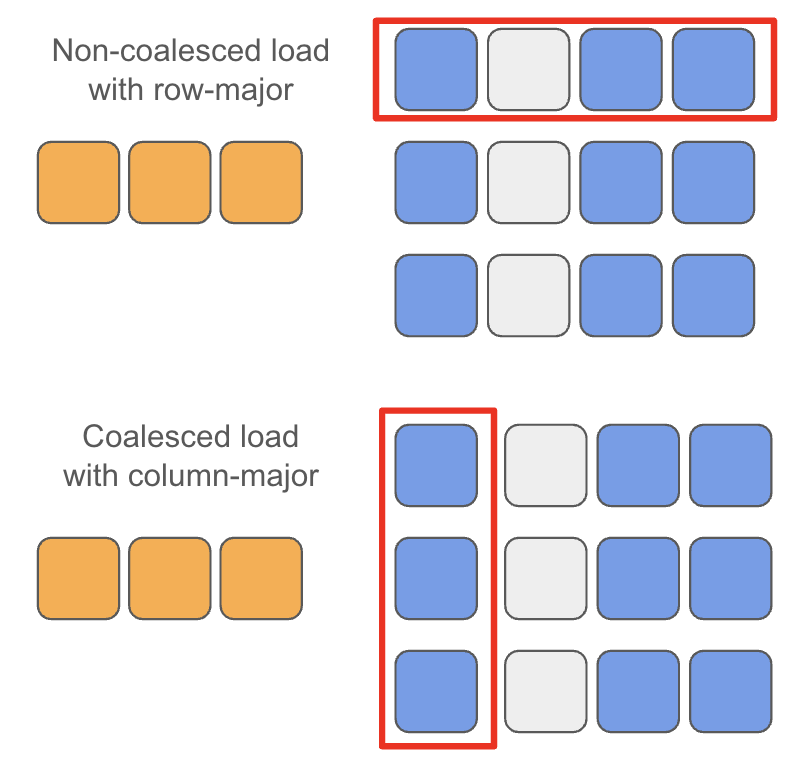
Obviously, we need to change B and C to column major matrices to make it more efficient.
Optimized Indexed GEMM
Let’s allocate B, C as,
B = torch.randn((N, K), device='cuda', dtype=torch.float16)
C = torch.zeros((N, M), device='cuda', dtype=torch.float16)
Then, we only need to “transpose” the stride of B, C in the kernel by,
def indexed_matmul_kernel(
# Pointers to matrices
a_ptr, b_ptr, c_ptr,
l_ptr,
# Matrix dimensions
M, N, K,
L,
# The stride variables represent how much to increase the ptr by when moving by 1
# element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
# by to get the element one row down (A has M rows).
stride_am, stride_ak, #
# NOTE: the only thing we need to do
# stride_bk, stride_bn, # B is transposed
stride_bn, stride_bk, #
# stride_cm, stride_cn, # C is transposed
stride_cn, stride_cm,
# Meta-parameters
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr, #
GROUP_SIZE_M: tl.constexpr, #
):
...
Because we transposed C, now the output looks like
# C =
tensor([[ 29.4531, -8.6953, -28.8438, ..., 4.7539, -22.7031, 5.6445],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[ 36.5625, -48.7500, 23.9062, ..., -21.1875, -40.3750, -15.5000],
...,
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[-15.2500, -27.9375, 8.2109, ..., -4.5234, 39.1562, -15.2422],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
device='cuda:0', dtype=torch.float16)
As you can see, only the selected “columns” are assigned values.
Results
The time consumption grows linearly with the size of index vector.
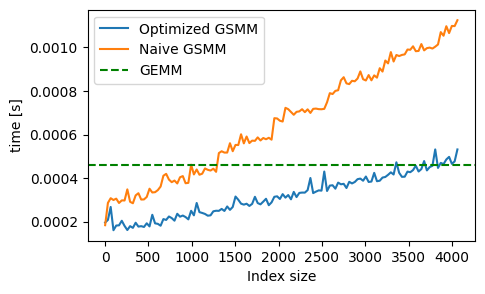
Final Implementation
Here is the final implementation in full code
import torch
import tqdm
import triton
import triton.language as tl
M, N, K = 512, 4096, 1024
a = torch.randn((M, K), device='cuda', dtype=torch.float16)
# `triton.jit`'ed functions can be auto-tuned by using the `triton.autotune` decorator, which consumes:
# - A list of `triton.Config` objects that define different configurations of
# meta-parameters (e.g., `BLOCK_SIZE_M`) and compilation options (e.g., `num_warps`) to try
# - An auto-tuning *key* whose change in values will trigger evaluation of all the
# provided configs
@triton.autotune(
configs=[
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5,
num_warps=2),
triton.Config({'BLOCK_SIZE_M': 32, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5,
num_warps=2),
# Good config for fp8 inputs.
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
],
key=['M', 'N', 'K'],
)
@triton.jit
def indexed_matmul_kernel(
# Pointers to matrices
a_ptr, b_ptr, c_ptr,
l_ptr,
# Matrix dimensions
M, N, K,
L,
# The stride variables represent how much to increase the ptr by when moving by 1
# element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
# by to get the element one row down (A has M rows).
stride_am, stride_ak, #
stride_bn, stride_bk, #
stride_cn, stride_cm,
# Meta-parameters
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr, #
GROUP_SIZE_M: tl.constexpr, #
):
"""Kernel for computing the matmul C = A x B.
A has shape (M, K), B, C are transposed as:
B has shape (N, K) and C has shape (N, M)
"""
# -----------------------------------------------------------
# Map program ids `pid` to the block of C it should compute.
# This is done in a grouped ordering to promote L2 data reuse.
# See above `L2 Cache Optimizations` section for details.
pid = tl.program_id(axis=0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
num_pid_n = tl.cdiv(L, BLOCK_SIZE_N)
num_pid_in_group = GROUP_SIZE_M * num_pid_n
group_id = pid // num_pid_in_group
first_pid_m = group_id * GROUP_SIZE_M
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
pid_m = first_pid_m + (pid % group_size_m)
pid_n = (pid % num_pid_in_group) // group_size_m
# ----------------------------------------------------------
# Create pointers for the first blocks of A and B.
# We will advance this pointer as we move in the K direction
# and accumulate
# `a_ptrs` is a block of [BLOCK_SIZE_M, BLOCK_SIZE_K] pointers
# `b_ptrs` is a block of [BLOCK_SIZE_K, BLOCK_SIZE_N] pointers
# See above `Pointer Arithmetic` section for details
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % L
offs_bl = tl.load(l_ptr + offs_bn)
offs_k = tl.arange(0, BLOCK_SIZE_K)
# offs_bl = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N) * 2
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bl[None, :] * stride_bn)
# -----------------------------------------------------------
# Iterate to compute a block of the C matrix.
# We accumulate into a `[BLOCK_SIZE_M, BLOCK_SIZE_N]` block
# of fp32 values for higher accuracy.
# `accumulator` will be converted back to fp16 after the loop.
accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
# Load the next block of A and B, generate a mask by checking the K dimension.
# If it is out of bounds, set it to 0.
a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
# We accumulate along the K dimension.
accumulator = tl.dot(a, b, accumulator)
# Advance the ptrs to the next K block.
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
c = accumulator.to(tl.float16)
# -----------------------------------------------------------
# Write back the block of the output matrix C with masks.
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = offs_bl
c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
tl.store(c_ptrs, c, mask=c_mask)
def indexed_matmul(a, b, c, index, activation=""):
# Check constraints.
assert a.shape[1] == b.shape[1], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
assert b.is_contiguous(), "Matrix B must be contiguous"
M, K = a.shape
N, K = b.shape
L = index.shape[0]
# print(M,K,N,L)
# 1D launch kernel where each block gets its own program.
grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(L, META['BLOCK_SIZE_N']), )
indexed_matmul_kernel[grid](
a, b, c, #
index,
M, N, K, #
L,
a.stride(0), a.stride(1), #
b.stride(0), b.stride(1), #
c.stride(0), c.stride(1), #
)
return c
index = torch.arange(0, N, 2).to('cuda')
b = torch.randn((N, K), device='cuda', dtype=torch.float16) # b is transposed
c = torch.zeros((N, M), device=a.device, dtype=torch.float16) # Allocates output.
triton_output = indexed_matmul(a, b, c, index)
torch.cuda.synchronize()
duration = 0
for i in range(100):
start = time.perf_counter()
triton_output = indexed_matmul(a, b, c, index)
torch.cuda.synchronize()
end = time.perf_counter()
duration += (end - start)
print(f"Indexed matmul full time {duration/100}s")
# print(triton_output)
avg_time = []
workloads = torch.arange(0, N, 32)
indices = torch.arange(0, N)
# shuffle index
indices = indices[torch.randperm(N)]
for wl in tqdm.tqdm(workloads):
# get index 0:wl and sort the indices in ascending order
index = indices[:wl].sort()[0].to('cuda')
duration = 0
for i in range(100):
start = time.perf_counter()
triton_output = indexed_matmul(a, b, c, index)
torch.cuda.synchronize()
end = time.perf_counter()
duration += (end - start)
torch.cuda.synchronize()
avg_time.append(duration/100)
# plot the time vs workload, workload = N/sparsity
import matplotlib.pyplot as plt
plt.plot(workloads, avg_time)
plt.xlabel('Workload')
plt.ylabel('Time')
plt.title('Time vs Workload')
# plt.savefig('time_vs_workload.png')
plt.show()
You may also try on Google Colab/triton_gather_scatter.ipynb

Comments